Toying Around With Powers of Two
Suppose I have a positive integer $x$ in base 10. It is possible to write $x$ as a sum of powers of two. This raises an interesting question: What is the minimium number of non-zero summands using the powers of two required to a given positive integer $x$?
For example, if the number was 9, the minimum number of summands of powers of two is 2 since $2^3 + 2^0 = 9$. If the number is 12, the minimum number is 2 since $2^3 + 2^2$.
We have stumbled upon the minimum Hamming weight problem in base 2. As such, let us define the minimum Hamming weight of a positive integer $x \in \mathbb{Z}^{+}$ as $M_{HW}(x)$.
When $x$ is a power of two (e.g., 1, 2, 4, 8, 16), $M_{HW}(x) = 1$. When $x$ is a power of two minus 1 (e.g., 7, 15, 31), we are forced to set all the previous powers of two to one in order to reach $x$. For instance $(1)2^0 + (1)2^1 + (1)2^2 = 7$ and $(1)2^0 + (1)2^1 + (1)2^2 + (1)2^3 = 15$. Therefore, when $x = 2^n - 1$ $\forall n \geq 2$, $M_{HW}(x) = n - 1$.
We know the bounds for the minimum hamming weight of any integer. Formally, for $x \in \mathbb{Z}^{+}$, $1 \leq M_{HW}(x) \leq n + 1$ where $n = \lfloor log_{2}(x) \rfloor$.
Given an integer $x$, let us write an iterative algorithm to compute $M_{HW}(x)$.
r = 0
while log2(x) not equal to 0
p = floor( log2(x) )
x = x - 2^p
r = r + 1
The value of $r$ at the end is $M_{HW}(x)$. This algorithm runs in $O(log x)$ because, at worst, we take $log_{2}(x)$ times through the while loop. Essentially, what we are doing here is converting $x$ to binary and counting the number of 1’s in the binary representation.
Is it possible to find a closed form analytical expression for $M_{HW}(x)$ such that we have a constant time solution, $O(1)$ to the problem?
Why would this be important? Minimum Hamming weights are used to generate secure cryptographic keys, discover DNA motifs, align DNA sequences, compress data, and detect errors in binary.
Let us graph the behavior of $M_{HW}(x)$
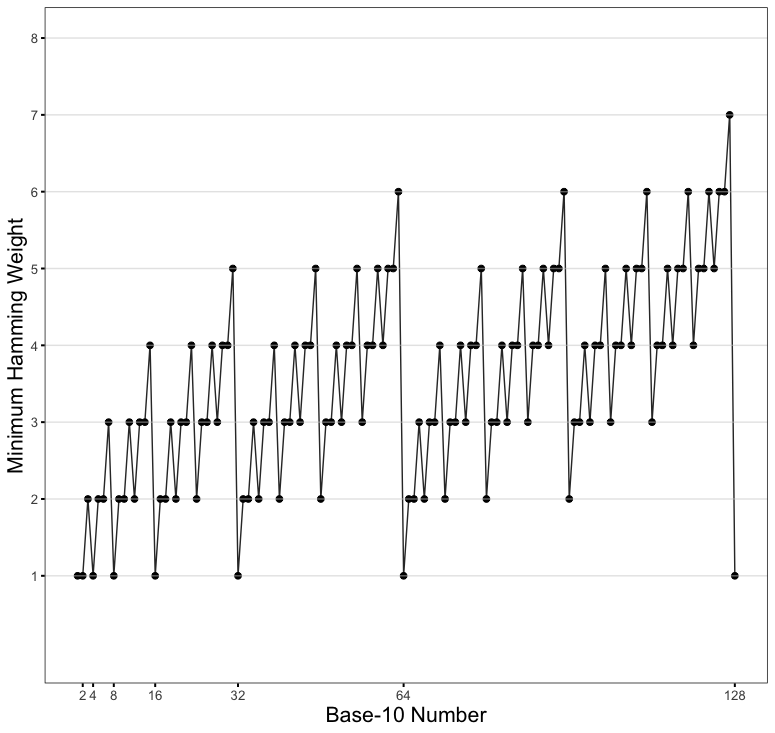
There is periodicity with a reset at each power of two. Observe the behavior of the Hamming weights on each interval:
(open interval) = {Hamming weights in that interval}
(2^1, 2^2) = {2}
(2^2, 2^3) = {2, 2, 3}
(2^3, 2^4) = {2, 2, 3, 2, 3, 3, 4}
(2^4, 2^5) = {2, 2, 3, 2, 3, 3, 4, 2, 2, 3}
The interval between $2^3$ to $2^4$ is a repeat of the previous interval $2^2$ to $2^3$ (2, 2, 3) plus a string of equal length three with the same structure incremented by 1 (3, 3, 4). This continues in that $(2^4, 2^5)$ has first half equal to that of the values on $(2^3, 2^4)$ and second half equal to that of the first half plus 1. Namely, take an integer $s = 2^k$. Let $v_i$ represent the value of the $i^{th}$ minimum Hamming weight in the open interval $(2^{k-1}, 2^k)$. Let $q_i$ represent the value of the $i^{th}$ minimum Hamming weight in the open interval $(2^{k}, 2^{k+1})$. We know that $v_i = q_i + 1$.
If asked to find $M_{HW}(x)$, we need $M_{HW}(2^{\lfloor log_{2}(x) \rfloor + 1} - x)$. Note that $M_{HW}(2^{\lfloor log_{2}(x) \rfloor + 1} - x)$ is the formal representation of the symmetrical windows discussed in the previous paragraph.
Of course, we can do this operation above recursively until we end up with an integer $y$ where we know $M_{HW}(y)$ and then exit the recursion by adding 1 equal to the number of loops we created. This is effectively the same complexity and solution as the pseudocode we wrote originally.
We seek a mapping that allows us to go from $x$ to $M_{HW}(x)$ without knowing any other $M_{HW}$ values on the open interval $(1,x)$. I am not sure this is possible.
ChatGPT 3.5 concurs:
No, it’s not possible to predict the Hamming weight of a number solely based on its base 10 representation. The Hamming weight is a property of the binary representation of a number, which depends on the position and value of its bits. The base-10 representation of a number does not provide any direct information about its binary representation, and therefore it cannot be used to predict the Hamming weight. To determine the Hamming weight of a number, you would first need to convert it to its binary representation and then count the number of nonzero bits.