Disappearing into the vacuum of elevators

How much of our time do we spend in the elevator? I am moving into the 17th floor of a building soon and wanted to understand how much time I will be spending waiting for elevators and in elevators. Up until this move, I have always lived in houses or places where using the stairs is easy and fast.

The time spent in an elevator to travel $x$ floors is given by $f(x) = k(x) + (2)(2)(c)$ where $c$ is the number of seconds it takes for the door to move either open or closed, $k$ is the number of seconds it takes to travel a floor, and there are 2 stops that happen at the entry and exit floors with both a closing and opening of the doors that takes place. What if we make $s$ total stops? Well, we now have $2(s)$ more door openings and closing. The expression is now: $f(x, s) = k(x) + 2(s)(c)$ where $s \geq 2$.

And, elevators take time to reach the floor you are on so there is some wait time $t$ built in there. We arrive at a final expression: $g(x, s, t) = k(x) + 2(s)(c) + t$.

We will investigate the form of $f(x,s)$ and then consider $g(x,s,t)$.

Let us consider the time spent in an elevator if you live in an apartment building as a graduate student. In general, how much more time does person A who lives on floor $y$ compared to person B who lives on floor $z$ assuming $y \geq z$? We must compute $\frac{f(x, s)_A}{f(x, s)_B}$ = $\frac{f(y, s_A)}{f(z, s_B)}$.

To answer this, we must consider the number of stops made between $n$, the floor the person lives on, and the ground floor. Basically, how many stops are made on the closed interval (1, n)? We can assume that the number of stops is a Poisson distributed random variable with parameter $\lambda$. For a Poisson, $\lambda$ is the mean number of stops per elevator trips. The mean number of stops is a function of the number of people waiting for the elevator. It is difficult to arrive at an estimate for $\lambda$ theoretically. But, we are only interested in the relative amount of time spent in an elevator assuming we choose to live on floor $z$ versus floor $y$. Therefore, the number of stops is now only a function of the number of floors to travel. Given the same amount and destinations of the people, if I live on a higher floor, I will have to make more stops en route to my destination. Thus, $\lambda$ is linear with the number of floors left to travel. $s_A \sim Poisson(y\cdot\lambda)$ and $s_B \sim Poisson(z\cdot\lambda)$ where $y,z$ are the floors that person A and B live on, $\lambda$ is a function of the number of people that are waiting to get on and off the elevator. On average, the ratio of the number of stops between person A and person B is $\frac{s_A}{s_B}$ which is equal to $\frac{y}{z}$ by the linearity of expectation.

What if we wanted to find the absolute number of stops for person A, on average? We want the expected value of $s_A$ which is $E[Poisson(y\cdot\lambda)] = y\cdot\lambda$. What is $\lambda$? We know that we must choose $\lambda$ such that no random sample from the Poisson can exceed $n$, the total number of floors, since the total number of stops cannot be greater than $n$. Poisson distributions have support from zero to infinity so the maximum is not well-defined, but we can at the least ensure that the mode of the Poisson does not exceed $n$ which means that $\lambda$ must be less than or equal to 1.

Finally, to arrive at $g(.)$, we must consider the time $t$ it takes for the elevator to reach the floor you live on. It depends on the number of elevators in the building. For simplicity, let us assume there is only one elevator. We want to find the time it takes to go from floor $q$ to $x$ where $q$ is the floor the elevator starts at and $x$ is the floor the person calls it from. Thus, $t = f(abs(x-q),s_{q,x})$.

What floor $q$ does the elevator come from? At any given moment, on what floor is the elevator? The probability distribution governing this likely has a large density on the ground floor and otherwise equal density on the other floors. It seems reasonaible that 90% of the time the elevator is at ground floor and the other 10% of the time it is evenly split across all the other floors. So the probability density $p(x)$ of where the elevator is at any given moment in time is $p(1) = 0.90$, and $p(x) = \frac{0.1}{n-1} \forall x \in {2,n}$. Without simulation, we can find $q$ by computing the average value of $p(x)$. To the nearest integer, the elevator will be on floor round(0.9*1 + sum(unlist(lapply(2:n, function(x) x*(0.1/(n-1)) ) ))). The 90-10 is just an assumption, it can be updated based on data. From here, the average number of stops between $q$ and $x$, $s_{q,x}$, can be computed by finding the expected value of the Poisson distribution with parameter $\lambda\cdot\lvert q-x \rvert$. Again, $t_A$ depends on $\lambda$ but the ratio $\frac{t_A}{t_B} = \frac{\lvert q-y \rvert}{\lvert q-z \rvert}$ is independent of $\lambda$.

We can partially account for multiple elevators by reweighting the probability density function above. Simply switch the densities given to $p(1)$ and $p(m)$ where $m$ corresponds to the default floor closest to the floor that the person lives on across all elevators. To make this clear, if there are three elevators with default settings of sitting at floor 1, 7, and 17 (e.g., Madison Towers in New Haven) when not in use, and the person lives on floor 15, then $m = 17$ and $p(m) = 0.9$; $p(1) = \frac{0.1}{n-1}$.

Let us use some real numbers for our constants. We will use data from the technical standards and safety authority. 2.5s seems like a good consensus estimate for how long it takes for a door to complete a movement (either opening or closing). And, from personal experience, 1.5s seems like a decent guess for how long it takes to travel one floor in an elevator.

Now, suppose there are 17 total floors, with three elevators positioned at floors 1, 7, and 17 as their defaults. How much time does a person who lives on floor Z spend on a given trip from floor Z to floor 1? So, $g_Z = Z\cdot k + 2\cdot s_Z \cdot c + k(Z - q) + 2\cdot s_{Z, q}\cdot c$ where $s_Z, q, s_{Z,q}$ are not constants. Let us now simulate many such trips to floor $Z$.

What might a decent choice of $\lambda$ be given the constraints we laid out above and our personal experience in elevators? For $s_Z$, the minimum of the distribution must not be lower than two since the elevator must stop on the floor the person enters and exits on at least. With this constraint, under the poisson, $P(0) = e^{-\lambda}$, $P(1) = e^{-\lambda} \cdot \lambda$, $P(2) = e^{-\lambda} \cdot \frac{\lambda^2}{2}$ must all take small values. Most of the random draws should be close to 2 with very few exceeding 5 from personal experience. Playing around with different choices of $\lambda$, 0.1 appears to be a good candidate. Lower values of $\lambda$ display better behavior for larger floor values $f$ making random draws from $Poisson(\lambda\cdot f)$ more realistic. Any random samples with values less than two are set back to two, the empirical lower limit. For $s_{Z,q}$, we do not enforce this minimum of two stops.

Here is some R code to perform the simulation.

library(tidyverse)

#number of trips to simulate
n <- 1000

#elevator constants
k <- 1.5
c <- 2.5
lambda <- 0.1
n_floors <- 17
rest_prob <- 0.9
elevator_defaults <- c(1, 7, 17)

#stochastic components of simulation
stochastic_components <- function(n_floors, floor_prob, elevator_defaults, lambda, Z, q, k, c){


	default_floor <- elevator_defaults[which.min(abs(Z - elevator_defaults))]
	floor_prob <- rep( (1-rest_prob)/(n_floors - 1), n_floors)
	floor_prob[default_floor] <- rest_prob

	q <- sample(x=c(1:n_floors), size=1, prob=floor_prob) 
	stops_on_elevator <- max(rpois(n = 1, lambda = lambda*Z), 2)
	stops_while_waiting <- max(rpois(n = 1, lambda = lambda*abs(Z-q)))

	time <- Z*k + 2*stops_on_elevator*c + k*(abs(Z - q)) + 2*stops_while_waiting*c

	time

}

#floors that people can live on
floors <- c(2:17)

#Let Z be the floor we are coming from / going to from the ground floor

times <- lapply(floors, function(Z) data.frame(time = (lapply(1:n, function(x) stochastic_components(n_floors, floor_prob, elevator_defaults, lambda, Z, q, k, c)) %>% unlist()), floor = Z))

times <- do.call(rbind, times) %>% as_tibble()

times %>% ggplot(aes(x=floor, y=time, group=floor)) + geom_boxplot(outlier.shape=NA) + geom_jitter(width=0.1, alpha=0.2, size=0.5, color="grey70") + theme_classic() + ylab("Time (s)") + xlab("Floor you live on") + ggtitle("Distribution of time spent in an elevator per trip in New Haven Madison Towers") + theme(plot.title=element_text(hjust=0.5)) + scale_y_continuous(n.breaks=10) + scale_x_continuous(breaks=c(2:17))

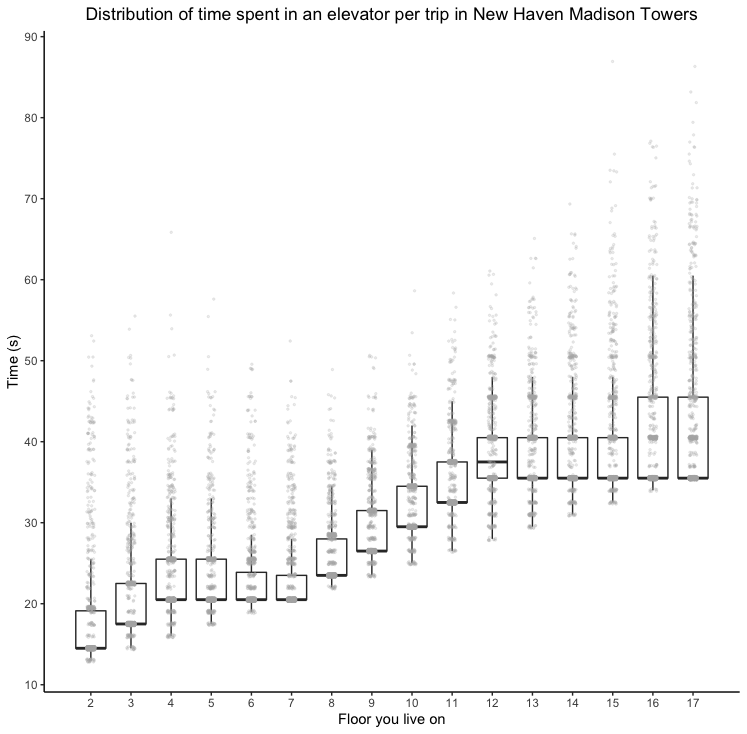
We simulate 1000 trips from a given floor and the ground floor and arrive at a distribution of times across floors people can reside on. On average, someone on floor 3 spends half as less time as someone on floor 11 in an elevator per trip. Those on floor 13 to 17 spend, on average, roughly the same time in an elevator. But, as expected, there is much larger variance for those on floors 16 and 17. Those on floor 12 spend more time on average in an elevator than those on floor 13 likely because the decision boundary for the default elevator lies on floor 12 in our model. The floor 7 and 17 default elevators are 5 floors from 12 but the floor 17 default elevator is only 4 floors from floor 13 reducing the time it takes to get an elevator when you press the button on average.

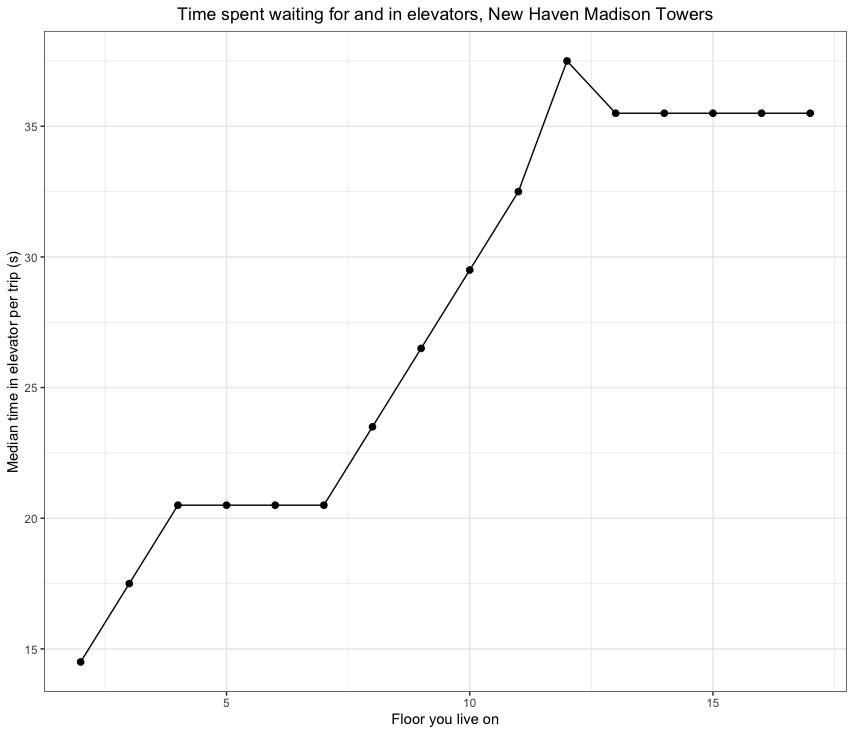
So, using the median time per trip which is robust to outliers, we see that someone on floor 17 spends 42s per trip and someone on floor 8 spends 26s per trip. How accurate is this? I took the elevator in Madison towers to floor 8 and timed it from pressing the button on the lobby and it took 29s. Not bad. This is only 1 data point though.

The absolute amount of time per day that you spend in an elevator depends on how often you enter and exit the floor you live in on. 6 trips a day is a conservative estimate - one when you leave in the morning, one when you come back for a meal/snack/errands/work, one when you go back down to attend an event or meet a friend, one when you come up to get ready to go to the gym, one when you go down to go to the gym, one when you come up and end your evening. It could be anywhere from 4 (alone time) - 10 (laundry day) in a given day.

If you live on floor 17, you could spend anywhere from 4 to 7 minutes a day waiting for and in an elevator. Over a month, that amounts to 2 to 3.5 hours! Over a year, that amounts to 24 to 42.5 hours - more than one entire day. That’s a lot of time that gets sucked into the vacuum of elevators.